Binary Tree Traversals are most common Tree Problems in an Interview as well as Competitive Programming. They can be efficient while searching, inserting and deleting compared to Linear Data structures (like Array, Linked Lists, Stacks, etc).
Trees can be traversed in many ways. Understanding traversing will help us solve complex searching in an efficient way with less time complexity.
While going through LeetCode Explore section of Binary Trees, I decided to document the Traversing of a Binary Tree so that it can be useful for myself while revisiting as well as it can be helpful for to our Coding Community.
A Binary Tree is a tree which has at-most two children. In this article we will see how we can implement Depth First Binary Tree Traversals along with Kotlin Examples.
Depth First Traversals:
- PreOrder Traversal
- InOrder Traversal
- PostOrder Traversal
Let us take an example Binary Tree and carefully look at each of the above traversals so that we can visualise and understand what happens during Tree Traversal.
Here is a Binary Tree formed with elements – 1,2,3,4,5.
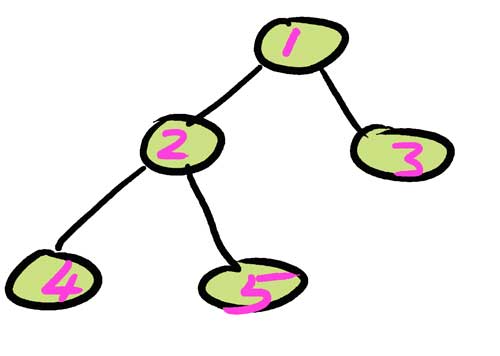
Creating a TreeNode and a Binary Tree
Let us try to create the above Binary Tree. Firstly we create a TreeNode which will help creating our Binary Tree. Our function initializeBinaryTree() will be called whenever we need to create a Binary Tree.
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| class TreeNode(var data: Int, var left: TreeNode? = null, var right: TreeNode? = null) | |
| fun initializeBinaryTree(): TreeNode { | |
| val c = TreeNode(4) | |
| val d = TreeNode(5) | |
| val a = TreeNode(2, c, d) | |
| val b = TreeNode(3) | |
| return TreeNode(1, a, b) | |
| } |
Now let us see each Depth-First traversals in detail.
PreOrder Traversal
In PreOrder Traversal, each node is processed before its child subtrees. That is why the name – PreOrder.
Here the order of traversal for the above example will be as follows: 1 2 4 5 3.
Let us now see how we can achieve the same through Recursion.
Recursive:
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| fun preorderTraversal(root: TreeNode?): List<Int> { | |
| // if root is null, return list of empty array | |
| if (root == null) { | |
| return listOf() | |
| } | |
| // iterate recursively into left child and right child | |
| return listOf(root.data) + preorderTraversal(root.left) + preorderTraversal(root.right) | |
| } |
As we can see, the recursive solution is Trivial and less asked in the interviews. Let us now see how we can achieve the same through Iterative Solution.
Iterative:
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| import java.util.ArrayDeque | |
| fun preOrderTraversalIterative(root: TreeNode?): List<Int> { | |
| val myList = mutableListOf<Int>() | |
| // creating stack to store the left and right nodes while processing root node | |
| val stack = ArrayDeque<TreeNode>() | |
| // checking edge case and returning empty list | |
| if (root == null) return myList | |
| var node = root | |
| while (node != null || stack.isNotEmpty()) { | |
| if (node != null) { | |
| stack.push(node) // pushing before processing children | |
| myList.add(node.data) //adding before going to left subtree | |
| node = node.left | |
| } else { | |
| val p = stack.pop() // now popping stack to traverse right subtree | |
| node = p.right | |
| } | |
| } | |
| return myList | |
| } |
The code is commented wherever it is necessary. Feel free to leave comments in case of any queries.
InOrder Traversal
Here, the root node is processed in between left and right sub trees. Hence the name InOrder Traversal. The order of output using the above binary tree will be: 4 2 5 1 3
Now let us see the recursive solution for InOrder Traversal
Recursive
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| fun inOrderTraversalRecursive(root: TreeNode?) : List<Int> { | |
| if (root == null) return emptyList() | |
| return inOrderTraversalRecursive(root.left) + listOf(root.data) + inOrderTraversalRecursive(root.right) | |
| } |
Here is the iterative Solution:
Iterative
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| import java.util.ArrayDeque | |
| fun inorderTraversalIterative(root: TreeNode?): List<Int> { | |
| val list = mutableListOf<Int>() | |
| if (root == null) return list | |
| var node = root | |
| val stack = ArrayDeque<TreeNode>() | |
| // traversing the tree whenever right node is not null or the stack contains items | |
| while (node != null || stack.isNotEmpty()) { | |
| // processing all the left nodes of the current node | |
| if (node != null) { | |
| stack.push(node) | |
| node = node.left //traversing to left node without processing root data | |
| } else { | |
| node = stack.pop() | |
| list.add(node.data) // adding to the list if no left child | |
| node = node.right // processing the right subtree | |
| } | |
| } | |
| return list | |
| } |
Post-Order Traversal
In PostOrder Traversal, the parent node will be processed after both child subtrees are processed.
The output of the above binary tree if processed using PostOrder Traversal will be: 4 5 2 3 1.
Here are the Recursive and iterative Solutions for PostOrder:
Recursive:
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| fun postOrderRecursive(root: TreeNode?) : List<Int>{ | |
| if(root == null) return emptyList() | |
| return postOrderRecursive(root.left) + postOrderRecursive(root.right) + listOf(root.data) | |
| } |
Iterative:
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| import java.util.ArrayDeque | |
| import java.util.LinkedList | |
| fun postOrderIterative(root: TreeNode?): List<Int> { | |
| if(root == null) return emptyList() | |
| val stack = ArrayDeque<TreeNode>() | |
| val list = LinkedList<Int>() | |
| stack.push(root) | |
| while (stack.isNotEmpty()) { | |
| val node = stack.pop() | |
| list.addFirst(node.data) | |
| node.left?.let { stack.push(it) } | |
| node.right?.let { stack.push(it) } | |
| } | |
| return list | |
| } |
Hope you find this Binary Tree Traversals in Kotlin article useful. Here is the GitHub Repo Link where the code is committed. Drop a Star if you like it. See you guys in our next article.


